CSES Math Problemset Tutorial

NOTE : It is incomplete, If you don’t find what you’re looking for, check back in a week.

So, there are total 31 problems, let’s solve them by the solve count.

Exponentiation⌗

Problem Statement

Given $a$ and $b$, calculate $a^b$ modulo $10^9+7$. Standard application of binary exponentiation.

int modp(int a,int b){
	if(b==0)return 1;
	int u=(1LL*u*u)%mod;
	if(b&1)return a*u%mod;
	return u;
}

Exponentiation II⌗

Problem Statement

Given $a$,$b$ and $c$, calculate $a^{b^{c}}$ modulo $10^9+7$.

Is $a^b$ multiplied with itself $c$ times equal to $a^{b^c}$?

No, it is equal to $a^{bc}$, as exponents get added while multiplying.

Can $b^c$ be reduced further?

According to fermat’s little theorem $a^{p-1} \equiv 1 mod p$, here $p$ being a prime integer.

So we can break down $b^c$ into some $x$ parts $p-1$ and an integer. $$b^c = (p-1)*x + r$$

Therefore, $$a^{b^{c}} = a^{(p-1)*x+r}$$

or $$a^{b^{c}} = a^{(p-1)*x}a^r$$

or $$a^{b^{c}} = a^r$$

How to find $r$ now? After finding $r$ it becomes same as first problem.

$r$ is remainder $b^c$ is divided by $p-1$.

Thus, it is equivalent to solving first problem twice, once raising $b$ to $c$ using $p-1$ as mod and then raising $a$ to $r$ using $p$ as mod. $p$ here is $10^9 +7$

const int mod=1e9+7;
int r=modp(b,c,mod-1);
int ans=modp(a,r,mod);
cout<<ans<<"\n";

Counting Divisors⌗

Problem Statement

Count number of divisors of $X$. There are about $10^5$ such queries in the largest test. It is trivial to find divisors of $N$ in $O(N\sqrt{N})$, and it will be very slow here because of the large number of such queries.

One observation is that we have to just count the number of divisors not find the exact divisors.

Can we do some pre-processing and answer all queries in O(1) after that?

Let’s keep a vector $dv$ where $dv[i]$ is number of divisors of $i$. Any number $i$ will contribute $1$ to $dv[j]$ such that $j$ is multiple of $i$.

So, if we update answer for multiples of $i$ by $1$ for every $i$, will it be fast enough?

Number of steps for calculating answers up to $n$ is $n + \frac{n}2 + \frac{n}3 + \cdots + \frac{n}n$.

It is equal to $$n \sum\limits_{x=1}^n \frac{1}x$$

or $$n \int \limits_{x=1}^n \frac{1}x = n log n$$

Therefore, it is fast enough to pre-process in $O(nlogn)$ and then answer queries in $O(1)$.

for(int i=1;i<N;i++){
	for(int j=i;j<N;j+=i)dv[j]++;
}
int t;cin>>t;
while(t--){
	int x;cin>>x;
	cout<<dv[x]<<"\n";
}

Common divisors⌗

Problem Statement

Find a pair of numbers in given array such that they have maximum gcd.

Equivalent to finding greatest divisor which divides at least 2 numbers in the given array. We already know how to count divisors of a number in given range, as done in previous problem. Here we have to count multiples of numbers from $1$ to $10^6$ which exist in the given array, then print the largest number which has at least two multiples in the array.

Code is similar to the previous problem.

const int N=1e6+1;
int available[N],ct[N],x,n;

cin>>n;
for(int i=1;i<=n;i++){
	cin>>x;
	available[x]++;
}

for(int i=1;i<N;i++){
	for(int j=i;j<N;j+=i){
		ct[i]+=available[j]; //update contribution of multiple
	}
}

for(int i=N-1;i>=1;i--){
	if(ct[i]>=2){
		cout<<i<<"\n";
		return 0;
	}
}

Sum of Divisors⌗

Problem Statement

Given a number $n$, calculate sum of all divisors of numbers in range $1$ to $n$ modulo $10^9+7$.

In previous problem we did count how many times a divisor occurs for given numbers in an array. Now, let’s say our array has all the numbers in range $[ 1,n]$. So once we get the frequency of all the divisors, it is a linear sum after that.

But, $n$ is too large to create an array and divisors will be very big too, obviously.

Unlike previous problem, all numbers from $1$ to $n$ are present here. Maybe this uniformity makes the problem easier for big $n$.

Number of multiples of $i$ in range $[1,n]$ is $\lfloor \frac{n}i \rfloor$.

Therefore, the answer to the problem for a given $n$ is

$$\sum \limits_{i=1}^n \lfloor\frac{n}i\rfloor * i$$

As $n$ can be as big as $10^{12}$. We can’t calculate this sum in linear time directly.

Here are some observations:

• We can calculate first $\sqrt n$ terms avoiding TLE verdict.
• After that $\lfloor\frac{n}i\rfloor$ takes only $\sqrt n$ distinct values.
• When $i$ changes in range $[ \sqrt n, n]$, then $\frac{n}i$ changes from $\sqrt n$ to $1$.
• $\frac {n}x$ is the largest value of $i$ for which $\lfloor\frac{n}i\rfloor$ is $x$.
• All $i \in [\sqrt n, n]$ such that $\lfloor \frac{n}i \rfloor = X$ is continuous.

For an integer $X$:

• $l$ is smallest value of $i$ such that $\lfloor \frac{n}i \rfloor = X$
• $r$ is largest value of $i$ such that $\lfloor \frac{n}i \rfloor = X$
• Contribution of the interval in $[\sqrt n, n]$ where $\lfloor \frac{n}i \rfloor = X$, can be written as: $$X ⋅ \sum \limits_{i=l}^r i = X ⋅ \Biggl( \frac{r*(r+1)}2 - \frac{l*(l-1)}2 \Biggr)$$

ll inv2=500000004;
ll n;
cin>>n;
ll inv2=modp(2,mod-2);
ll ans=0;
for(int i=1;i*i<=n;i++){
	ans=(ans+(1LL*(n/i)*i)%mod)%mod;
}
ll l=sqrtl(n);
l++; //left is 1+right of the last value
for(ll val=l;val>=1 ;val--){
	ll r=n/val; //r can be as large as n
	ll contribution = (r%mod)*((r+1)%mod)%mod;
	if(r<l)continue; //zero contribution when interval is non-existent
	ll left = (l%mod)*((l-1)%mod)%mod;
	contribution = (contribution -left + mod)%mod;
	contribution = (contribution*inv2)%mod;
	contribution = (contribution*(val%mod))%mod;
	ans=(contribution+ans)%mod;
	l=r+1;
}
cout<<ans<<"\n";

Binomial Coefficients⌗

Problem Statement

Many queries of the form $n$ and $r$ calculate $C(n,r)$ modulo $10^9 +7$

calculate factorial and inverse factorial in advance and then answer all queries in $O(1)$.

f[0]=1;
int ncr(int n,int r){
	if(n<r)return 0;
	int res=1LL*f[n]*inv[r]%mod;
	return 1LL*res*inv[n-r]%mod;
}

Creating Strings II⌗

Problem Statement

How many different strings can be formed from the characters of given string?

Here, using its characters means that all characters are to be used. So we have to print number of all valid permutations of given string.

Let’s suppose all characters are distinct in a string of length $N$, then answer is $N!$. If $X$ characters are same out of $N$ then number of distinct permutations will be $\frac {N!}{X!}$ because after making $X$ characters same, we counted identical permutations $X!$ times.

vector<int> h(26);
string s;
cin>>s;
for(auto i:s)h[i-'a']++;
int ans=f[s.length()];
for(int i=0;i<26;i++){
	ans=ans*inv[h[i]]%mod;
}

Distributing Apples⌗

Problem Statement

Ways to distribute $m$ apples among $n$ children. It is possible that someone gets nothing. Consider $n-1$ partitions and $m$ apples are to be arranged together. Now every arrangement can be considered as a possible distribution. Apples to the left of $i_{th}$ partition are number of apples $i_{th}$ child gets, and number of apples to the right of last partition is the number of apples the last child gets.

It is equivalent to arranging $n-1$ characters of one type and $m$ characters of another type in a string. We just solved a similar problem above.

int n,m;
cin>>n>>m;
int ans=f[n-1+m]*inv[m]%mod;
ans=ans*inv[n-1]%mod;
cout<<ans<<"\n";

Christmas Party⌗

Problem Statement

It is equivalent to finding how many ways are there such that a gift doesn’t leave with the same child it came to party with, and every gift can be with exactly one child. Therefore it is equal to counting the number of derangements of size $N$.

Now there is a recurrence for counting derangements. Let’s say $D(n)$ is number of derangements of size $n$. Then

$$D(n) = (n-1)(D(n-1) + D(n-2))$$

Consider gift at position $1$ we have $n-1$ choices to replace it with, suppose we replaced it with $x$. After that either we can put $1$ at place of $x$ and then calculate $D(n-2)$, or we can put some other gift at place of $x$ and calculate $D(n-1)$.

d[1]=0;
d[2]=1;
int n;cin>>n;
for(int i=3;i<n;i++){
	d[i]=1LL*(i-1)*(d[i-1]+d[i-2])%mod;
}
cout<<d[n]<<"\n";

Fibonacci Numbers⌗

Problem Statement

Find $n_{th}$ fibonacci number, here $n$ can be as large as $10^{18}$, so $O(n)$ approach won’t work. Can be calculated by matrix exponentiation. Further reading on matrix exponentiation

ll n;cin>>n;
ll fib[2][2]={{1,1},{1,0}},ret[2][2]={{1,0},{0,1}},tmp[2][2]={{0,0},{0,0}};
int i,j,k;
while(n){
	if(n&1){
		memset(tmp,0,sizeof tmp);
		for(i=0;i<2;i++)
			for(j=0;j<2;j++)
				for(k=0;k<2;k++){
					tmp[i][j]=(tmp[i][j]+ret[i][k]*fib[k][j])%mod;
				}

		for(i=0;i<2;i++)for(j=0;j<2;j++)ret[i][j]=tmp[i][j];
	}

	memset(tmp,0,sizeof tmp);
	for(i=0;i<2;i++)
		for(j=0;j<2;j++)
			for(k=0;k<2;k++)
				tmp[i][j]=(tmp[i][j]+fib[i][k]*fib[k][j])%mod;

	for(i=0;i<2;i++)for(j=0;j<2;j++)fib[i][j]=tmp[i][j];
	n/=2;
}

cout<<ret[0][1]<<"\n";

Throwing Dice⌗

Problem Statement

Ways to get sum $n$ by throwing a dice. Let’s say answer for $n$ is $T_n$.

$$T_n=T_{n-1} + T_{n-2} + T_{n-3} + T_{n-4} + T_{n-5} + T_{n-6}$$

As we can only get the values in range $[1,6]$, so these are the only penultimate states.

Here again $n$ can be as large as $10^{18}$. It is similar to how we calculated fibonacci numbers, but with extra terms.

ll n;cin>>n;
ll mat[6][6]={{1,1,1,1,1,1},
		{1,0,0,0,0,0},
		{0,1,0,0,0,0},
		{0,0,1,0,0,0},
		{0,0,0,1,0,0},
		{0,0,0,0,1,0}};
ll ret[6][6]={{1,0,0,0,0,0},
		{0,1,0,0,0,0},
		{0,0,1,0,0,0},
		{0,0,0,1,0,0},
		{0,0,0,0,1,0},
		{0,0,0,0,0,1}};
ll tmp[6][6];
int i,j,k;
while(n){

	if(n&1){
	memset(tmp,0,sizeof tmp);
	for(i=0;i<6;i++)
		for(j=0;j<6;j++)
			for(k=0;k<6;k++){
				tmp[i][j]=(tmp[i][j]+ret[i][k]*mat[k][j])%mod;
			}

	for(i=0;i<6;i++)for(j=0;j<6;j++)ret[i][j]=tmp[i][j];

	}
	memset(tmp,0,sizeof tmp);
	for(i=0;i<6;i++)
		for(j=0;j<6;j++)
			for(k=0;k<6;k++)
				tmp[i][j]=(tmp[i][j]+mat[i][k]*mat[k][j])%mod;

	for(i=0;i<6;i++)for(j=0;j<6;j++)mat[i][j]=tmp[i][j];

	n/=2;
}
cout<<ret[0][0]<<"\n";

Graph Paths I⌗

Problem Statement

Given a directed graph with $n$ nodes find out number of paths from node $1$ to $n$ with exactly $k$ edges.⌗

Adjacency matrix of an graph has an interesting property. When $A$ is adjacency matrix of a graph, then $A^k[i][j]$ contains the number of paths of length $k$ from $i$ to $j$.

You can see it is true when $k$ is $1$. Adjacency matrix is essentially populated with number of paths of length $1$ between every pair of nodes.

How to be sure that it is true for higher powers?⌗

It can be proved by using principle of mathematical induction.

We know that it is true for $k=1$

Suppose it is true for any $k=x$, now $A^x[i][j]$ is number of paths of length $x$ from $i$ to $j$.

Let’s call number of paths of length $x+1$ from $i$ to $j$ as $C_{x+1}[i][j]$.

Every path from $i$ to $j$ of length $x+1$ will surely be extending a path of length $x$ by $1$. Now from every intermediate node $y$ where path of length $x$ from $i$ ends, we need to find number of paths of length $1$ starting from $y$ and ending at $j$. Therefore, we can write

$$C_{x+1}[i][j] = \sum\limits_{y=1}^n A^x[i][y] ⋅ A[y][j]$$

Thus, $C_{x+1}$ is equal to multiplying $A^x$ and $A$, more precisely $A^{x+1}$.

To solve the problem, we’ll create an adjacency matrix for the given graph, call it $A$ and then print $A^k[1][n]$ as the answer.

cin>>n>>m>>K;
for(i=0;i<m;i++){
	cin>>u>>v;
	u--;v--;
	adj[u][v]++;
}
for(i=0;i<n;i++)ret[i][i]=1;



while(K){
	if(K&1){
		memset(tmp,0,sizeof tmp);
		for(i=0;i<n;i++)
			for(j=0;j<n;j++)
				for(k=0;k<n;k++){
					tmp[i][j]=(tmp[i][j]+ret[i][k]*adj[k][j])%mod;
				}
		for(i=0;i<n;i++)for(j=0;j<n;j++)ret[i][j]=tmp[i][j];
	}

	memset(tmp,0,sizeof tmp);
	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
			for(k=0;k<n;k++){
				tmp[i][j]=(tmp[i][j]+adj[i][k]*adj[k][j])%mod;
			}
	
	for(i=0;i<n;i++)for(j=0;j<n;j++)adj[i][j]=tmp[i][j];

	K/=2;
}

cout<<ret[0][n-1]<<"\n";

Graph Paths II⌗

Problem Statement

In a weighted graph of $n$ nodes. Find the minimum path length from $1$ to $n$ with exactly $k$ edges.

It can be solved by using similar dp we used in the problem above.

Let’s say $C_{x}[i][j]$ is minimum path length of $x$ edge path from $i$ to $j$.

Then, we can write $$C_{x+1}[i][j] = \min\limits_{k=1}^n C_{x}[i][k]+C_{1}[k][j]$$

cin>>n>>m>>K;
for(i=0;i<n;i++)
	for(j=0;j<n;j++){ret[i][j]=adj[i][j]=inf;}
for(i=0;i<m;i++){
	cin>>u>>v>>w;
	u--;v--;
	adj[u][v]=min(adj[u][v],w);
	ret[u][v]=adj[u][v];
}
K--;
while(K){
	if(K&1){
		for(i=0;i<n;i++)for(j=0;j<n;j++)tmp[i][j]=inf;
		for(i=0;i<n;i++)
			for(j=0;j<n;j++)
				for(k=0;k<n;k++){
					tmp[i][j]=min(tmp[i][j],ret[i][k]+adj[k][j]);
				}
		for(i=0;i<n;i++)for(j=0;j<n;j++)ret[i][j]=tmp[i][j];
	}

	for(i=0;i<n;i++)for(j=0;j<n;j++)tmp[i][j]=inf;
	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
			for(k=0;k<n;k++){
				tmp[i][j]=min(tmp[i][j],adj[i][k]+adj[k][j]);
			}
	
	for(i=0;i<n;i++)for(j=0;j<n;j++)adj[i][j]=tmp[i][j];

	K/=2;
}

if(ret[0][n-1]>=inf)puts("-1");
else
cout<<ret[0][n-1]<<"\n";

Dice Probability⌗

Problem Statement

What is the probability that sum of the outcomes of rolling a 6-faced dice $n$ times is in range $[a,b]$?

Let’s solve a simpler problem first.

What is the probability that sum of outcomes is $X$, if we roll a dice $n$ times? As distance between $a$ and $b$ is very less we can add up answers to all the numbers between $a$ and $b$.

Let $dp[i][j]$ be probability of getting sum $i$ in $j$ rolls.

So, $$dp[i][j] = \sum\limits_{x=1}^{min(j,6)}\frac{dp[i-1][j-x]}6$$

After calculating dp table, final answer of the problem will be $\sum\limits_{i=a}^bdp[n][i]$

int n,a,b;cin>>n>>a>>b;
dp[0][0]=1.0;
for(int roll=1;roll<=n;roll++){
	for(int sum=1;sum<=roll*6;sum++){
		for(int lst=1;lst<=min(6,sum);lst++){
			dp[roll][sum]+=dp[roll-1][sum-lst];
		}
		dp[roll][sum]/=6.0;
	}
}
double ans=0;
for(int i=a;i<=b;i++)ans+=dp[n][i];
printf("%.6lf",ans);

Bracket Sequences I⌗

Problem statement

Calculate the number of valid bracket sequences of length $n$.

Here, the total length of the sequence is $n$. So there won’t be any valid sequence when $n$ is odd because we’ll not have equal number of opening and closing brackets.

So what are the necessary and sufficient conditions to create a valid bracket sequence of length $n$.

• Equal number of opening and closing brackets
• At every point number of closing brackets must be less than or equal to number of opening brackets.

Therefore after printing 0 for every odd $n$, we needn’t care about first condition. Now, we have $\frac{n}2$ opening brackets and $\frac{n}2$ closing brackets and have to find number of valid bracket sequences using all of them.

Thus we have two kind of moves - Use $)$ or $($, and there is a limit on their use, each move can be used exactly $n/2$ times.

We can model this problem to an equivalent grid walking problem.

There is a grid (as shown in the figure below), you are standing at $(0,0)$ and the destination is $(\frac{n}2, \frac{n}2)$, count total possible paths such that you can only move up i.e. use “$)$” exactly $\frac{n}2$ times and move right i.e. use “$($” exactly $\frac{n}2$ times.

But, what about the condition that at every moment : $$closing\space brackets \leq opening \space brackets$$ can be rephrased as: $$moves\space in \space upward \space direction \leq moves \space to \space the \space right$$

It means that no point in the possible valid paths will be above anti-diagonal. In the figures below, figure to the left shows a valid path, as it is entirely below the diagonal, and the figure to the left shows an invalid path as it overshoots diagonal at point $P$.

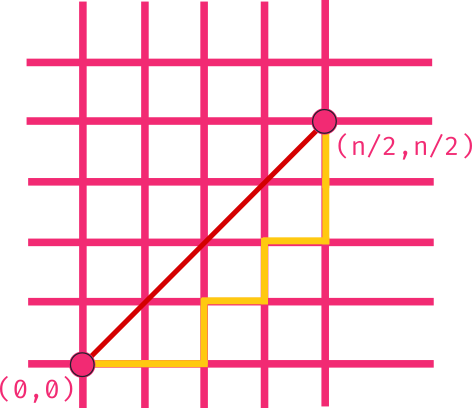
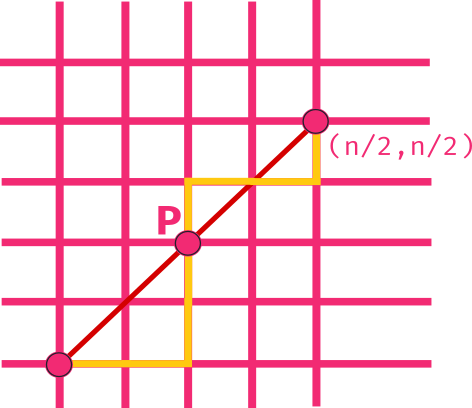
How to count these good paths?

Total possible paths irrespective of the conditions imposed by the diagonal are ${}^n C_{\frac{n}2}$ So, if we can somehow count all the paths that overshoot the diagonal at some point, we can subtract them from total to get the count of good paths.

When a path crosses the diagonal for the first time, let’s call it $k_{th}$ move. Note that $k$ here is odd because it is the first time up moves become greater than right moves. Till $k_{th}$ move, we already have used exactly, $\frac{k-1}2$ right moves and $\frac{k-1}2 + 1$ up moves.

We are left with $\frac{n}2 - \frac{k-1}2$ right moves and $\frac{n}2 - \frac{k-1}2 - 1$ up moves.

PLEASE PAY ATTENTION NOW (MAGICAL STEP OF THE PROOF)

Now, for every move if we go up whenever the invalid path goes right and go right whenever the invalid path goes up, then sum of the moves in both directions becomes constant again.

What do we get by making the sum of moves constant?

It means that now any invalid path can be mapped to a path from $(0,0)$ to a fixed position in the grid, and we know how to calculate number of possible paths between two points in a grid, if we have only two kind of moves.

What is that fixed point?

In essence we swapped the number of right moves left and number of up moves left with each other.

By doing so,$$total \space right \space moves = \frac{k-1}2 + \frac{n}2 - \frac{k-1}2 -1 = \frac{n}2 - 1$$

And, $$total \space up \space moves = \frac{k-1}2 + 1 + \frac{n}2 - \frac{k-1}2 = \frac{n}2 + 1$$

So final position every time would be $(\frac{n}2 -1 , \frac{n}2 +1)$, as shown in the figure below

Therefore number of such paths is ${}^nC_{\frac{n}2 -1}$

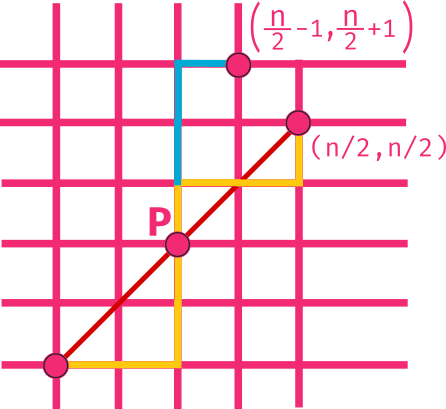
Therefore answer is $$Total\space paths - bad \space paths = {}^nC_{\frac{n}2} - {}^nC_{\frac{n}2 -1}$$

cin>>n;
if(n&1){
	puts("0");
	return 0;
}
int total=ncr(n,n/2);
int bad=ncr(n,n/2+1);
int ans=(total-bad+mod)%mod;
cout<<ans<<"\n";

Bracket Sequences II⌗

Problem Link

Instead of just the number $n$, you are also given a prefix of the sequence, how many valid ways are to complete this sequence such that it becomes a valid bracket sequence of length $n$.

Let $O$ be number of opening brackets in the prefix and $C$ be number of closing brackets in the prefix.

Re-frame this problem to previously seen grid walking problem

You are standing at $(O,C)$ on the grid, how many ways are there to reach $(n/2, n/2)$ such that you always remain below the straight line connecting $(n/2, n/2)$ and $(0,0)$.

So, $Total \space Paths = {}^{n-(O+C)}C_{\frac{n}2-O}$, irrespective of any condition.

Again, all invalid paths can be mapped to paths from $(O,C)$ to $(\frac{n}2 -1, \frac{n}2 +1)$

Thus, $Bad \space paths = {}^{n-(O+C)}C_{\frac{n}2 - O -1}$

First we check if the prefix is valid, i.e. it is under the diagonal, and number of opening brackets and closing brackets is less than $\frac{n}2$.

If prefix is not valid, answer is $0$.

else, it is $Total \space paths - Bad \space paths$

string s;cin>>s;
int o=0,c=0;
bool valid=1;
for(auto i:s){
	if(i==')')c++;
	else o++;
	valid&=(c<=o);
}
valid&=(c<=(n/2));
valid&=(o<=(n/2));
if(!valid or n&1){
	puts("0");
	return 0;
}

int total=ncr(n-(o+c), n/2-o);
int bad=ncr(n-(o+c), n/2-o-1);
cout<<(total-bad+mod)%mod<<"\n";